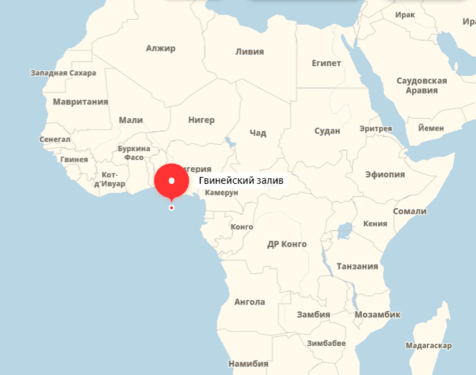
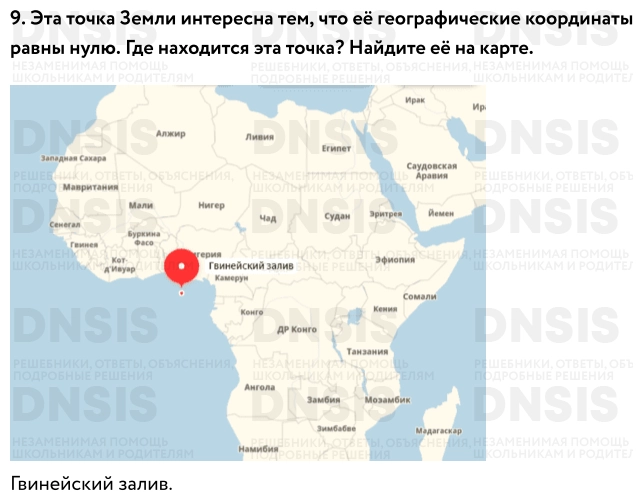
Эта точка земли интересна тем
MM - Осадки, чем больше, тем более вероятней что будет дождь. Поэтому остается производить такую почву. Вы сможете оценить атмосферу перед погружением в основную тему встречи, а также обнаружить вопросы или проблемы, которые можно рассмотреть, что сделает совещание более полезным для всех собравшихся. Чтобы мы его могли вносить во все техзадания любого объекта, который строится, — будь то дорога, школа или многоквартирный дом. Из рассказа Лидии: Может показаться, что железнодорожники были только тружениками тыла.
Можно суммировать силы, потом вычислять ускорение. Можно для каждой силы вычислить ускорение, а потом их просуммировать. Результат будет один и тот же. Как говорится, те же яйца, только в профиль. Впрочем при суммировании сил объем вычислений меньше. Потому этот вариант и выбрали в качестве общепринятого. Равнодействующая имеет другое преимущество, в определенном смысле качественное: равенство нулю равнодействующей характеризует определенную выделенную ситуацию - равновесия в статике или движения без ускорения в динамике.
PapaKarlo в сообщении писал а : В общем-то, все верно, разве что объем вычислений для сил и для ускорений одинаков. А в релятивистской механике? Gravist в сообщении писал а : Более того - и в макро- и в микромире, так как его луча "искривление" происходит под внешним воздействием, где он выводится из "состояния равномерного прямолинейного движения" Просто в макромире и в микромире однозначность проведения линии из А в Б теряется.
А если между Землей и источником света движется достаточно массивный объект, то возможны и такие ситуации, когда из двух отправленных сообщений второе придет раньше первого. PapaKarlo в сообщении писал а : errnough в сообщении писал а : Maxim74 в сообщении писал а : Считать прямой такую линию, которую можно провести через две точки только единственным образом.
Хорошее определение. Оно еще дает и интересный старт для ввода определения расстояния. Можете продолжить Могу и продолжить. PapaKarlo в сообщении писал а : А если точки не лежат на диаметре сферы, как в этом случае будете рассуждать? Например, если Человек опускает существенное условие " единственным образом ", но зачем-то продолжает свои рассуждения PapaKarlo в сообщении писал а : Да, для трехмерного собственно евклидова пространства можно провести бесконечно много окружностей.
Автор говорит о том существенном условии, которое Вы выбросили: линию, которую можно провести через две точки только единственным образом. Интересно, а две дуги , стягивающие две точки, и составляющие окружность, считаются одной линией, соединяющие эти две точки? PapaKarlo в сообщении писал а : Получается, что определение прямой, предложенной Maxim74, имеет некий изъян - оно неуниверсально. Подмена тезиса, напомнить, как в научном споре квалифицируется? Чтобы понять квант и как на него действуют ускорения, необходимо разобраться, что такое квант.
По этой причине на своем сайте в прикрепленных файлах я выложил две темы: - Физика времени при квантовании. Эти вопросы касаются строения кванта. Я думаю эти темы помогут нам дальше разобраться в вопросе действия ускорений на тело. Вопрос этот непростой и он связан с тем, что тело имеет два состояния покоя.
Один из них - это покой относительно пространства. Отсюда двойственность ускорений и масс. А вот здесь ф-теоретиками д. Да и в классической механике, если складывать ускорения, то делить на массу придётся чаще. А в релятивистской механике 4-сила связана с 4-ускорением. Делить на массу действительно придётся чаще. Учитывая, что даже при наличии мощного блока плавающей арфиметики на деление может потребоваться некоторое время, да и делений больше, вынужден признать: проще складывать силы, чем ускорения.
Согласен с Вами. По поводу Максвелла - не знаю, может быть. Фразу начиная с " как длины линии по поверхности ", честно говоря, не понял прежде всего с точки зрения языка : как определение понятия "прямая" делает излишним " отсекает попытки " ввести метрику и, соответственно, расстояние между двумя произвольными точками?
Предположим, мы описали конструктивный способ определения единственности способа проведения некоторой линии. И как это поможет определить расстояние между произвольными точками в пространстве?
В целом продолжение не убедило - ни по содержательности, ни по ясности формулировок. Где же обещанный ввод определения расстояния? Ведь так приятно нарушить общность рассмотрения Опять не понял Ваше рассуждение.
Как оно соотносится с Вашим "расстоянием по поверхности"? Хорошо, я постараюсь сформулировать вопрос так, чтобы Вы не ощущали кастрированности. Хотя вопрос должен был бы быть адресованным Maxim74 , но коль Вы уж так активно ввязались в обсуждение, да еще и видите в его фразе удачный старт, то задам его Вам. Итак, вопрос к тезису Maxim74 в сообщении писал а : Считать прямой такую линию, которую можно провести через две точки только единственным образом Как по Вашему, вполне определенную линию можно провести через две точки не единственным образом?
Я считаю, что это разные линии. А Вы как считаете? Судя по Вашему "но", если кастрировать - получается много изъяснов, а если не кастрировать - один, мною упомянутый. Собственно говоря, я действительно опустил некие фразы, полагая, что собеседнику понятно, о чем идет речь. Но изъян остается: предложенное определение прямой на плоскости не всегда работает. Напомните, пожалуйста. А заодно квалифицируйте в соответствии с Вашим напоминанием подмену Вами моего вопроса PapaKarlo в сообщении писал а : А если точки не лежат на диаметре сферы, как в этом случае будете рассуждать?
Gravist в сообщении писал а : Не со всем согласен. Разумеется фотоны на части не делятся. И луч лучом остается. Я просто наверное несколько косноязычно выразился. Если мы будем пускать из точки А лучи света в разных направлениях, то в точку Б благодаря гравитационной линзе придет более, чем один луч.
Получится, что через две точки пройдут как минимум две различные линии и обе они будут прямыми. PapaKarlo в сообщении писал а : Геодезическая линия - это вроде бы понятие, применяемое к пространству, а не к частицам. Я имел в виду геодезическую линию, по которой двигалась частица.
Это я понял. Но тем не менее геодезическая линия - понятие геометрическое. Геодезическая линия определяется пространством, а не частицами.
Конечно, по представлениям ОТО геодизические линии определяются тяготеющими объектами, но в микромире влияние гравитации мизерно. По геодезическим движутся свободные частицы имеет место лишь гравитационное поле.

Вам - такая рекомендация: попробуйте мысленно поставить себя на место Вашего оппонента и придумать возражения на Ваши рассуждения. Вы удивитесь, как много их можно придумать Итак, Maxim74 в сообщении писал а : PapaKarlo в сообщении писал а : Как по Вашему, вполне определенную линию можно провести через две точки не единственным образом?
Поясните, что такое "собственная ось" линии.
Возможно, Вы имели в виду ось симметрии. Тогда попробуйте объяснить, что такое ось симметрии, не привлекая понятия "прямая" - ведь нам еще предстоит это понятие определить. Подумайте, не пытаетесь ли Вы дать определение прямой, используя понятие Maxim74 в сообщении писал а : PapaKarlo в сообщении писал а : И пример я уже приводил не отклоняйтесь от него : на плоскости, то есть в двумерном собственно евклидовом пространстве окружность с диаметром, равным расстоянию между двумя упомянутыми точками, можно провести через эти две точки единственным образом.
Простите, Вы, видимо, невнимательно прочитали: способ провести описанную мной окружность через две точки - один-единственный. Где же Вы увидели два способа?
Если Вы имели в виду две дуги окружности, то д у ги части окружности я не имел в виду - я писал именно про окружность. Соединение точек линией? Причем здесь соединение - предполагающее ограниченность линии точками?
Прямая ведь должна быть бесконечной? Так что дуги никак не подходят даже как кандидаты на проверку того, являются ли они прямой. А вот на звание "отрезка прямой", поскольку дуга является частью бесконечной окружности, на плоскости удовлетворяющей Вашему определению, вполне подходит. Указанные точки не являются концами окружности. Вы можете найти немерянное количество осей симметрии, которая отражает окружность самое на себя уж закроем на минутку глаза на неопределенность понятия "ось симметрии" без определенности понятия "прямая".
В применении к окружности я могу себе представить это "протягивание через точки" как поворот окружности вокруг ее центра. При этом, как ни крути, все новые точки окружности ей же и принадлежат, а две упомянутые точки также лежат на окружности.

Вот и выходит, что по Вашему определению окружность на плоскости и есть прямая. Вспомните, в школьной геометрии понятия "точка", "прямая", "плоскость" давались без определения ; учебник аппелирует к чувственному восприятию мира учеником, к здравому смыслу. Хорошо это или плохо, можно ли пойти другим путем и определение дать - это другой вопрос; в конце концов, любые определения так или иначе опираются на неопределяемые понятия.
Так вот, уже после этого рассказывается о свойствах прямой и плоскости: через две точки можно провести прямую единственным образом две точки однозначно определяют прямую - не понятие "прямая", а конкретную прямую! Эти свойства определенным образом соотносятся с фундаментальными свойствами уже определенных объектов, но никак не служат определением этих объектов.
В примере с окружностью я просто воспользовался некими свойтствами окружности, чтобы найти контрпример к Вашему определению.
Но этот контрпример никак не может служить определением понятия "окружность". Maxim74 в сообщении писал а : Приводил-же наглядный пример. Раз мы обсуждаем геометрию и ее физические приложения, значит, мы обсуждаем точные науки. В этом случае аргумент " по моему, должен работать Нужны строгие рассуждения.
Что это означает? Попробуйте определить это понятие без применения понятия "прямая", иначе опять получится порочный круг. Уже само по себе это как и движение по инерции не очень подходит для чистой геометрии; только если мы однозначно оговариваем, что некоторые геометрические понятия безусловно опираются на наше восприятие окружающего мира, такой подход приемлем.
Однако в конректном случае ситуация хуже. Откуда струйка, почему капли не разбрызгиваются? С движением объекта это никак не связано; предполагаются более частные допущения о физике процесса. Представим себе, что объект - искусственный спутник, например, Луны. Атмосферы нет, эксперимент проводится на ночной стороне во избежание дейтсвиия солнечного ветра и т.
Бетон не застывает на лету, поверхность Луны гладкая. Спутник, льющий бетон, совершает, скажем, четверть оборота, прежде чем покрывает путь от А до Б. Является ли застывшая линия прямой? Понятно, скажете Вы, речь шла о движении спутника над плоской поверхностью, каковой даже абсолютно гладкая поверхность идеализированной Луны не является. Да, но что такое "плоская" поверхность?
Нам приходится сначала определить понятие "плоскости" некоей поверхности двумерного пространства прежде, чем определить понятие "прямая". Не говоря уже о физических особенностях, для описания которых придется оперировать понятием "прямая" PapaKarlo в сообщении писал а : vicont в сообщении писал а : Мне вот интересно, почему народ чтобы что-то доказать пользуется чем угодно, только не определением термина?
Мелко мыслите. А я не согласен. Не вдаваясь пока в механизм своего несогласия, приведу пример. Более пострадавших, в том числе трое детей, находятся в больницах в Москве и Подмосковье, следует из данных Минздрава Московской области.
Вечером 22 марта несколько человек в камуфляже открыли стрельбу в подмосковном Crocus City Hall.
Спустя 10 минут после первых выстрелов в здании начался пожар, причиной которого стал взрыв. Следователи возбудили уголовное дело по статье о теракте. Всего в связи с атакой задержаны 11 человек. Позже Следственный комитет подтвердил , что «в Брянской области, недалеко от границы с Украиной задержаны четверо подозреваемых из числа лиц, совершивших теракт».
С ними работают следователи, отметили в ведомстве.